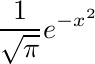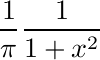Not so much an explanation of autism as a concise way of describing its symptoms: Autistic people do not spontaneously behave in unusual ways. Furthermore, they are more than usually surprised by the unusual ("outliers"). In a novel situation, normal people ignore unusual elements and concentrate on those elements that are like previous situations, but autistic people are unable to ignore these unusual elements. These two differences, in behaviour and sensitivity, are pervasive.
One can pose this hypothesis more precisely. Here is a draft paper that does so:
It rambles a bit, I am afraid, and needs tightening and restructuring.
Abstract:
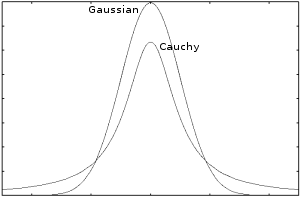
Autistic people are unusually sensitive to the unusual. Furthermore, their own behavior lacks spontaneous outliers. Autistic people stick to strict routines and their speech is flat and monotonous, or alternatively their behavior and speech is too variable but still lacks outliers. This absence may be what gives rise to an impression of "oddness". In this paper, a model of sensitivity to outliers in terms of the alpha-stable family of distributions is developed. In particular the Gaussian distribution, which is sensitive to outliers, is contrasted with the Cauchy distribution, which is not. This is used to conjecture the origins of sensory hyper-sensitivities, hearing impairments in noisy environments, pedanticism, difficulty understanding metaphors, "weak central coherence", unusual interests, impairments in understanding emotional cues, and communicative deficits. A simple random walk model of behavior is also developed, with autistic people characterized by an absence of spontaneous outlier steps.
Context: people as Bayesian modellers
The Bayesian approach to modelling: We have a bunch of possible models of the world. One of them is "true", but we don't know which, so the best we can do is try to estimate how likely each model is. To do this, we start with an initial distribution of how likely each model is that is as close to unbiassed as possible, and then as we observe new data we update the distribution to take it into account.
Such a distribution of models can then be used to make decisions: The utility of a given action can be estimated by summing the utility of that action given that the world is like each possible model, weighted by that model's current estimated likelihood. Choose the action with the greatest utility.
People are, approximately, Bayesian modellers.
But what types of model do people use?
For continuous valued observations, a nice generic scheme is mixture modelling. Model the observed data as a mixture of various "classes", each class having a position and spread. Let the classes have a fixed shape (eg Gaussian). I call this generic, because whatever the shape of class we use, we can approximate any distribution of values arbitrarily well by just adding more classes.
So if this is a generic scheme, the actual class shape doesn't matter, right? Well, actually yes it does, because we're being Bayesian. A Bayesian approach needs to start with a distribution of possible models. It would be nice, in order to be as unbiassed as possible, to be able to say that a model comprising i classes is just as likely as one comprising j classes. But we can't do that, because we don't have an upper bound on the number of classes -- if we said each number of classes was equally likely, the likelihood of any given number of classes would have to be zero. So we're pretty much forced to say models with few classes are more likely than models with many classes.
Here's the key point: Having observed exactly the same data, if two Bayesian modellers are using different class shapes, they will have different expectations as to which models are likely. Even if you disregard the internal structure of the models, and just look at what they predict about future observations, these two Bayesian modellers will differ.
Suppose most people modelled the world one way, but a few modelled it some other way. Here's some things we can say right away, without even knowing how they differ:
- These people will have a harder time understanding how normal people are thinking. Normal people will be good at modelling the models in other normal people's heads, and these different people will be good at modelling the models in the heads of others of their kind. But the different people won't be good at modelling how normal people think, and normal people won't be good at modelling how the different people think.
- These people will will be surprised by different things. They will pay attention to different things.
- The above two points mean that establishing shared attention between a normal and different person will be hard. Inferences such as "people point to surprising things" will be harder, because those things aren't necessarilly what these different people find most surprising.
I claim that this is exactly what is going on in autism. Difficulty with "theories of mind" and shared attention are key symptoms of autism.
Indeed, from this viewpoint, it's pretty easy to work out exactly how autistic people differ from normal.
The Hypothesis
Hypothesis: People people use Lévy alpha-stable statistical distributions to model variation. The autistic spectrum is due to variation in the shape parameter α that particular people use.
|
|
Comparing these extremes is sufficient to explain many autistic traits.
Note 1: Perhaps people use a different family of models. The more familiar Student t distribution also varies between these extremes. The alpha-stable family seems to me to have the best theoretical justification, however the key point is the difference between thin and thick tails.
Note 2: if you want to work with these distributions yourself, you might use my PyLevy python package.
Paragraph lengths
(section deleted)
I tried looking for a statistical signature in the paragraph and sentence lengths of writing by autistic people. On reflection, I'm unconvinced by the results. Too many confounding factors, eg dialog vs non-dialog text.
Relation to statistics and formal logic
The Gaussian distribution is the most widely used distribution in statistics and modelling.
Examples:
- The mean as a measure of central tendency
- Model estimation via least squares regression
- Gradient descent optimization of artificial neural networks
- k-means algorithm
- Self-organizing maps
- Noise modelling in control systems
How about logic?
To model boolean logic, lets consider a simple mixture model in one dimension, with two classes, the classes having the same spread but different center points. Given that a datum belongs to one of these classes, what is the likelyhood that it belongs to class A?
- If Gaussian distributions are used:
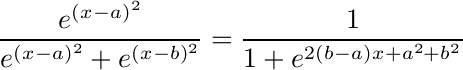
This is the logistic function often used in neural network models.
-
If Cauchy distributions are used:
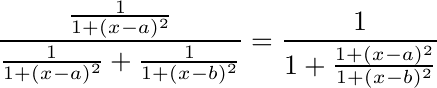
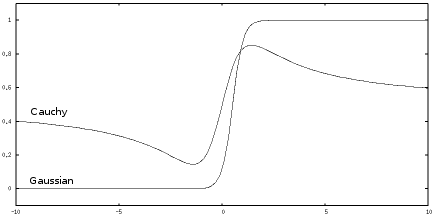
The Gaussian model says outlier data strongly belongs to the class it is nearer to, whereas the Cauchy model says outlier data could belong to either class. It would be hard for a neural network that used the Cauchy curve to implement boolean logic. The Gaussian based curve can be made as close as you like to a sharp binary discrimination, and is much better for implementing boolean logic. Models with more classes and dimensions can be made similarly sharp edged. This agrees with the observation that autistic people are often overly logical.
So our currently used techniques for statistics and formal reasoning might be said to have autistic qualities, and to lack common sense. The same holds for devices such as computers that automate these techniques.