pfh's blog: code section

28 October 2012, 20:30 UTCDemakein 0.2 release: shawms
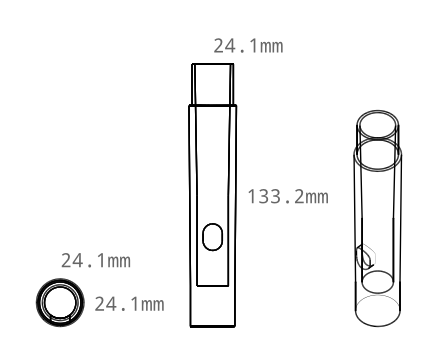
I've just released version 0.2 of my woodwind instrument maker. This version adds a shawm designer/maker. The bore shape optimization for the shawms was rather tricky, so the numerical optimzer has also undergone a complete overhaul.

Demakein homepage

Demakein PyPI page

Having printed a shawm, you can use my drinking-straw reed making method to make a reed for it:

Drinking straw reed making on Instructable

Soprano tapered folk flute, black strong and flexible

[permalink]

2 October 2012, 11:59 UTCAnnouncing Demakein
I have finally gotten the latest iteration of my woodwind design software to a state where I can release it.

The notable feature of this iteration is that it is able to produce shapes for 3D printing or CNC milling.

Demakein

Demakein on PyPI

Some instrument designs on Thingiverse

Demakein can currently design flutes in a number of styles. I will be adding other instruments such as shawms and reedpipes in the next few weeks.

Demakein uses the the nesoni tool writing framework to provide a collection of tools that can either be run from the command line or from Python, and that can be easily customized by subclassing in Python. For example you could subclass one of the flute designer tools and adjust some of its parameters.

[permalink]

23 September 2012, 0:13 UTCTalking to C++ for the incurably lazy

So I had been eyeing the Computational Geometry Algorithms Library for some time. It is a very beautiful thing, it's the kind of thing C++ was designed to allow and it really shows C++'s full potential. It's the library that powers the popular CAD program OpenSCAD, amongst other things. However, I rather like Python.

I saw that the makers of PyPy had come out with a C Foreign Function Interface. Again the stuff they're doing with PyPy is very beautiful, and this is characteristically elegant, it takes Python to first-class citizen status in the programming world, and under PyPy has the potential to be blisteringly fast.

But CGAL is not written in C, could never be written in C, is deeply, inextricably a thing of C++. C might sometimes be enough for code that internally uses C++, but here I really needed a way to talk C++ like a native. Now there are plans to collide Python and C++ using libraries used in high energy physics, but these are not yet in an easily usable state. So in the meantime I came up my own.

It is not beautiful.

But it gets the job done. It compiles snippets of code to interface C to C++ on the fly, using cmake. The compiled code is loaded on the fly using CFFI. Return types are inferred using typeid() and a utility called "c++filt". Simple types are converted to python equivalents, more complex types are boxed.

cpp.py

Goodbye Blender, with your inexact and fallible floating point numbers and your rough-and-ready meshes. Hello mind-melting perfect world of CGAL!

[permalink]

27 March 2010, 15:02 UTCSoftware to position the finger holes on a wind instrument
I wrote some software to calculate the positions of finger holes on a cylindrical wind instrument. If this is something you want to do, check it out.

This is to accompany a lesson I am giving on medieval and renaissance wind instruments at Suth Moot II this easter.

Update 10/4/2010: New version, with cross-fingering optimization.

[permalink]

27 December 2009, 22:48 UTC(melodic] clojure

Lisp! An elegant language from a more civilized age. Yet there has always been the matter of having to count brackets, the difficulty of seeing which bracket goes with which.

Users of Lisp and its children cope with this in various ways:

Indentation.

Writing only small functions.

Turning common nested chains of function calls into a single function call. For example, cond can stand for a chain of ifs, and let for a series of assignments.

Arranging the order of parameters to a function so that the most complex parameter is the final one.

This final method is effective, but still requires counting back the brackets at the end of a function. Text editors help with this, but would it not be nice if you did not need the text editor's help to understand your code?

Suppose we add a tiny bit of syntactic sugar that lets us express a list

(a b c)

(a b] c

with the final element of the list after the closing bracket.

I tried this in Clojure, and found the result pleasing. Consider quicksort (from Rosetta Code).

(defn qsort [L]
  (if (empty? L) 
      '()
      (let [[pivot & L2] L]
           (lazy-cat (qsort (filter (fn [y] (< y pivot)) L2))
                     (list pivot)
                     (qsort (filter (fn [y] (>= y pivot)) L2))))))

See how it drifts right. See the final )))))). See how the simpler case is handled first in the if, putting the meat at the end. Now let's apply sugar:

(defn qsort [L]]
(if (empty?] L '()]
(let[ [pivot & L2] L
    ]]
(lazy-cat (qsort] (filter (fn[y]] (< y pivot)] L2
          (list] pivot
          (qsort] (filter (fn[y]] (>= y pivot)] L2)

Note how the function is revealed to be a series of qualifications -- this is qsort, what to do in the base case, some variable definitions -- to a final statement of how to decompose sorting into two smaller sorting problems. Within each line, you can also see similar transformation into series of qualifications. No more )))))), the structure can be seen at a glance.

The let here is a little ugly, it would be nicer to be able to write:

(let variable-name value]

and simply use multiple let statements for multiple assignments.

You'll also note I left the comparisons unsugared. I feel the order of parameters would ideally be reversed for numerical operators. For example, (< pivot] y. Or for an average (/ (count] values] (sum] values. The denominator is usually less meaty than the numerator.

Another example, the Mandelbrot Set task from Rosetta Code:

(ns mandelbrot
  (:refer-clojure :exclude [+ * <])
  (:use (clojure.contrib complex-numbers)
        (clojure.contrib.generic [arithmetic :only [+ *]]
                                 [comparison :only [<]]
                                 [math-functions :only [abs]])))

(defn mandelbrot? [c]]
(loop [ iters 1
        z c
      ]]
(if (< 20] iters  
    true]
(if (< 2] (abs] z
    false]
(recur (inc] iters] (+ c] (* z] z

(defn mandelbrot []]
(apply str]
(interpose \newline]
(for [y (range 1 -1 -0.05)]]
(apply str]
(for [x (range -2 0.5 0.0315)]]
(if (mandelbrot?] (complex x y)
    "#"] 
" "

(println] (mandelbrot)

Download

Here is the patch to Clojure:

melodic.patch

Here is a Clojure jar with the patch applied (compiled from git repository as at 19 December 2009):

melodic-clojure.jar

If you have installed Java, you can use it with:

java -cp melodic-clojure.jar clojure.main

Why Melodic Clojure?

My initial application for this notation was writing musical melodies. For example, this is the music for the Buffens:

F ((G] A] (A] Bb 
A ((G] A] (F] G 
F ((G] A] (A] Bb 
A ((F] G] (G] F

c (d] (c] Bb
A ((G] A] (Bb] c
c (d] (c] Bb
A ((F] G] (G] F

After desugaring, the brackets indicate the division of time before each note. Before desugaring, the brackets indicate the emphasis pattern, the prosody. The deeper bracketed notes are given reduced emphasis.

--> See Metrical Phonology. For Melodic Clojure perhaps follow these rules:

(a b c] is a compound, the Compound Stress Rule applies, giving emphasis to a. Example: (apply +]

(a] (b] c is a phrase, the Nuclear Stress Rule applies, giving emphasis to c. Example: (println] (reverse] x

Where a-b-c is more like a compound than a phrase, prefer sugarless (a b c) to (a b] c. Example: accessing a member of an object, (table :leg)

[permalink]

5 August 2009, 11:14 UTCNew bioinformatics software: nesoni, and updated treemaker key-value store
I just put some code I've been working on at work up on the web. Nesoni is Python / Cython software for analysing high-throughput sequencing data. If you have huge piles of high-throughput sequencing data, especially of bacterial genomes, you might find it useful.

Nesoni

It's still fairly alpha. There's not a lot of documentation, but it's getting everyday use.

Perhaps of more interest to those of you who don't have to deal with huge steaming piles of high-throughput sequencing data, nesoni includes an updated version of the "treemaker" key value store I described in a previous blog post. Treemaker is useful for huge steaming piles of data of any kind! Treemaker excels at fast random writes. A simple example application would be an always live, always up-to-date inverted index.

This new version can perform merges in the background, using the multiprocessing module. It can happily keep several CPUs busy when under heavy load.

Treemaker is my secret sauce. For example, I've recently been using it to map paired end sequencing data onto a de Bruijn graph layout, using an inverted index from k-mers to read-pairs. This isn't yet part of nesoni, but should hopefully be part of a future version. The Velvet Assembler could probably be rewritten using treemaker, to remove its current excessive memory demands. I am, kind of by accident, about a quarter of the way to having done this.

[permalink]

6 June 2009, 22:38 UTCA key-value data warehouse

Grand sale! Grand sale!

Welcome to Paul's crazy data warehouse.

Everything reduced!

So here we are in 2009. Disks got big, but they didn't get fast. We have so much memory now that it takes a titanic amount of data to even start hitting the disk. But when you hit that wall, oh boy do you feel it.

I happen to be working with sequencing data that's just brushing up against that wall. Annoying.

Scattered reads and writes are agonizingly slow now. It's like the era of tape all over again. Flash storage solves this for the read side of things, but you still want coherent writes.

So, I've written myself a key-value store with this in mind. It's the flavour of the month thing to do.

Basic concept:

Merge sort can be performed with serial reads and writes. We'll maintain a collections of sorted lists, progressively merging lists together in the background. Writing data is simply a matter of adding a new list to this mix. Reading is a matter of checking each list in turn, from latest to earliest, for the key you want.

Refining things a little:

For random access to a database, you want items that are accessed with about the same likelihood to be stored near each other (ie in the same disk block). This way, your memory cache mostly contains frequently accessed items.

So I store each list as a balanced binary tree, with each level of the tree stored in a separate file. The list merging operation only ever needs to append to the end of each of these files, so this is still coherent writing.

Levels of the tree nearer the root will be accessed more often, and should end up in the memory cache. In-order traversal of the list remains fairly nice, since each level remains in order.

This scheme is cache oblivious, it works well with any size disk block. Which is handy, because you don't know jack about disks.

There is some room for improvement here, perhaps a trie.

Some nice properties:

Writing is fast. Chuck it on disk, merge at your leisure. In parallel, because this is 2009 and CPUs have stopped getting faster but there are plenty of them.

Multi-Version Concurrency Control is trivially easy. With only a little work, it will be impossible for the database to become corrupted. And it's backup-friendly.

You don't need to look up a record in order to modify it. For example, if you want to append to a record or add to a counter, you can set things up so this is deferred until merge-time. Each key effectively becomes its own little reduce. For example, you can implement a very nice word counting system this way. Which is exactly what I need for my sequencing data.

Implementation:

My implementation is not terribly optimized, but it is written in Cython, and is at least within the ballpark of reasonable. You'll need a recent Cython, and for Python 2.5 you'll also need the "processing" library.

I batch up key-value pairs in an in-memory dict until I have one million of them, before sorting them and writing them to disk. Python hashtables are fast, it would be silly not to use them until we are forced not to. One million items seems to be about optimal. This is a long way from filling available memory... something to do with cache size perhaps?

The performance on my machine is about 10x faster for writing than bsddb, 2x faster for reading, but still about 10-20x slower than an in-memory Python dict.

It's far from polished. Just proof of concept for the moment.

treemaker-0.2.tar.gz

As examples, version 0.2 contains:

General_store, supporting set, delete, and append operations. {set x} + {append y} -> {set xy}, {append x} + {set y} -> {set y}, {set/append x} + {delete} -> {delete}, {delete} + {set/append y} -> {set y}

Counting_store, for word counting.

Update 2/8/2009: This paper appears to be describing the same idea.

Update 5/8/2009: nesoni includes an updated version of treemaker.

[permalink]

21 February 2009, 6:24 UTCQuerying intervals efficiently in SQL + Python revisited
My previous post on querying intervals generated quite a lot of interest, but my solution was a hideous thing involving trinary numbers. I now have a better solution.

To recap: I am interested in efficiently finding, from a set of intervals, all intervals that contain a given value. I have quite a lot of intervals, so I want to use an SQL database to store and query these intervals.

By efficiently, I mean faster than O(n). Simply scanning the list is too slow, and indexing the upper and/or lower bound still yields an O(n) search.

It would furthermore be nice to be able to find all intervals that intersect a given query interval. My new solution allows this.

My new solution:

For each interval, store the upper and lower bounds, and the size of the interval rounded down to the nearest power of two (I'll call this value size). Create indexes on (size,lower) and (size,upper).

To perform a query, we consider each possible value of size (up to the maximum size interval you expect). Since size is at least half the true size of the interval, intervals that contain a certain value must satisfy either

lower <= value <= lower+size

upper-size <= value <= upper

or possibly both. We can efficiently find intervals satisfying these two conditions using the two indexes we have created. No mess, no fuss!

If your query itself is an interval, the two conditions become:

lower <= query_upper and query_lower <= lower+size

upper-size <= query_upper and query_lower <= upper

Implementation in Python/SQLite:

interval_query.py

SQLite needs a little coddling when implementing this. You need to convert value <= lower+size to value-size <= lower, etc, for it to use the indexes properly. explain query plan is your friend.

Update: Istvan Albert pointed me to this paper on Nested Containment Lists, which solve the same problem and are also amenable to SQL database implementation, and also this discussion of python interval database/query implementations on the pygr mailing list.

Performance notes:
The python file above generates a test data set of 1,000,000 intervals and performs 100 queries on it. On my machine, my method is 20 times faster than just using an index on (upper, lower).

I've also tried this on set of 15,000,000 alignments of Illumina short reads to a reference bacterial genome. On my machine, with my method a query retrieving 500 alignments takes 0.009 seconds, as compared to 27 seconds just using an index on (lower, upper), or 49 seconds with no index at all.

[permalink]

18 February 2009, 6:17 UTCQuerying intervals efficiently in SQL + Python
Update 21/2/2009: See my new solution to this problem here.

I have a problem where I need to be able to efficiently[1] find all of the intervals that contain a particular (integer) value. There are data-structures to do this efficiently, for example the interval tree. However, I have quite a lot of intervals, and I don't want to have to code up a complicated disk-based data structure, so I am constrained to use a database.

The solution I came up with is to assign each interval a particular numerical code, such that a query of a small set of such codes will guarantee finding each interval that contains a given value.

I'm not sure if this is novel. It seems a fairly obvious thing to do, so probably not. If not, can anyone tell me what it is called?

The code is this: I produce a trinary number from the binary representation of the lower and upper bounds of the interval. Starting with the most significant digit I map 0->1 and 1->2 until the first digit that varies between the lower and upper bounds. From there on I just produce 0s.

An example may make this clear:

Lower  00010101010
Upper  00010101111

Output 00021212000

To perform a query, I similarly convert the binary query number to trinary. The query set is then this trinary number with each least significant digit converted to zero in turn.

An example:

Query  00010101100

Output 00021212211
       00021212210
       00021212200
       00021212000
       00021210000
       00021200000
       00021000000
       00020000000
       00000000000

Here's the source code:

range_codes.py

The source code includes code to test this idea using SQLite.

Update: This is hideous. Sorry. I am working on a much nicer scheme, stay tuned.

[1] Clarification: By efficiently I mean faster than O(n).

[permalink]

18 January 2009, 20:50 UTCSketchifier

Click image to see original.

sketch.py

Requires Python 2, Python Imaging Library, Numpy.

The basic principle is to draw lines but not corners or dots. Lines, and corners and dots can be detected by the eigenvalues and determinant of the Hessian respectively. I also need to blur the image for various reasons, which I attempt to do in as scale-free a way as possible by using a long tailed convolution kernel (of course, you know I'm obsessed by these things), a t-distribution to be precise.