My previous solution needed four linker tiles. I've now found a way to get rid of these. Each tile simply transmits the state of the tile above it to its left and right neighbours.
These tiles implement Rule 30:
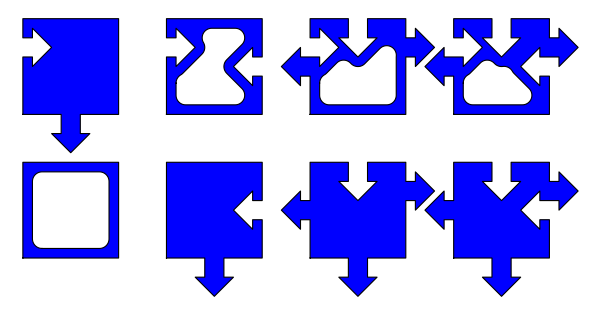
- Filled tiles are "on" and empty tiles are "off".
- Downward arrow on the base transmits the state to the cell below.
- Outward sideways arrows transmit state of N neighbour to E and W neighbours.
- Inward pointing arrows receive state of NW neighbour via W neighbour, state of N neighbour, and state of NE neighbour via E neighbour.
Seed tile:
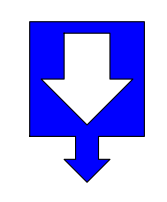
Starting from this seed in the middle of a line of empty squares, the puzzle has a single, infinite solution. The column of tiles below the seed passes tests of randomness used to test pseudo-random number generators. Rule 30 is used as a random number generator in Mathematica. Rule 30 is a simple demonstration of Stephen Wolfram's observation that mathematics is random, and that "creating information" is trivial.
I previously speculated about making these tiles from plastic. Technology to do this is now readily available.

Source code:
Requires Python 2, "shapely" python library. Produces files for OpenSCAD in a directory "output". Usage:
python cell_tiles.py 30
You might also like to try other elementary cellular automata, such as Rule 110 which is a computer.