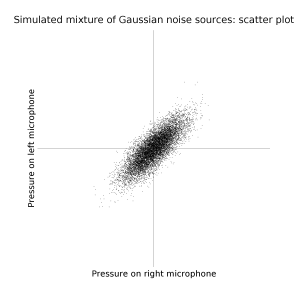
Consider the problem of separating a set of sound sources based on multiple simultaneous recordings (eg stereo). For example, with two sources and two microphones, one might rotate the recording such that the sources are seperated into independant channels.
If the sounds have a Gaussian volume profile, and one sound is louder than the other, the recording will be an ovoidish multivariate Gaussian, and a good guess to the separation might be the principal components of this ovoid.
If the sounds are Gaussian and of about the same loudness, you are stuffed.
Update... er, actually even if they're different loudnesses you're still stuffed. Oopsie. The principle components will always be orthogonal, but the sound sources may not be.
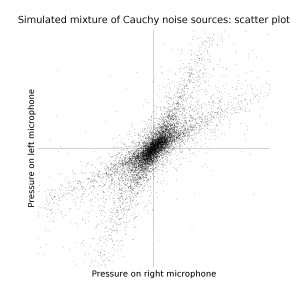
But sounds usually aren't Gaussian, they have fat tails. If you were to plot the density, it would be kind of sucked in along directions not aligned with the noise sources.
The usual approach to this seems to be to find the rotation such that the seperated sources have the least mutual information. I haven't done a full literature survey, but they seem to be measuring statistical moments to achieve this. Foolish Earth humans, they do not realize that higher order moments are rarely finite. (To be fair, it seems this is a recognized problem, and fractional moments are therefore sometimes used... hmm...)
You can guess where this is going. Multivariate Levy stable distributions. And the fact that autistic people have difficulty with noisy environments suggests this is in fact the form of analysis that people use: Autistic people, modelling the noises with distributions of high alpha (ie Gaussianish), will have less of that sucking in effect to go on. Normal people, modelling noises using low-alpha Cauchyish distributions, will have far less difficulty.
See also: John Nolan's page on stable distributions. Especially overview.ps (Figure 1 is a good example of the sucking in effect).
Ah, here we go... "Blind separation of impulsive alpha-stable sources using minimum dispersion criterion".