2017-11-08

Outline

Consider the problem of finding differentially expressed genes from RNA-seq data.

  1. Review FDR adjusted p-values

  2. Travel to a parallel universe of FDR adjusted confidence bounds

  3. Confident effect sizes for interactions

Null Hypothesis Statistical Test

A procedure that will reject a null hypothesis only with small probability \(\alpha\).

eg "This gene's expression has log fold change \(e\)."

Binary outcome: reject or do not reject.


Ways to give the reader more freedom:

  • Only fix \(e\), usually \(e=0\). Tell the reader a \(p\)-value. The reader may choose their desired \(\alpha\), and rejects the null hypothesis if \(p \leq \alpha\).

  • Only fix \(\alpha\), usually \(\alpha=0.05\). Try all possible \(e\) and tell the reader the set non-rejected values, which form a Confidence Interval or a Confidence Bound.

False Discovery Rate control

(Benjamini and Hochberg, 1995)

For a False Discovery Rate of \(q\), given \(p\)-values \(p_1\)…\(p_n\), find the largest set \(S\):

\[ S = \left\{ i : p_i \leq {|S| \over n} q \right\} \]



Snowballing: The more discoveries you make, the lower the threshold for discovery.

A happy medium

No adjustment for multiple testing

  • \(S = \left\{ i : p_i \leq q \right\}\) – expect \(nq\) false discoveries

False Discovery Rate control

  • \(S = \left\{ i : p_i \leq {|S| \over n} q \right\}\) – expect \(|S|q\) false discoveries*

Family-Wise Error Rate control

  • \(S = \left\{ i : p_i \leq {1 \over n} q \right\}\) – expect \(q\) false discoveries
*actually a worst case expectation, holds when the number of true discoveries to be made is \(\ll n\)

FDR "adjusted p-values"

Allow the reader to choose FDR.

The set of genes with adjusted \(p\)-value \(\leq q\) controls FDR to be \(q\).

Presentation as a "top table": If genes are sorted by \(p\)-value, whatever \(q\) is chosen the set will always be the head of the table.

Snowballing: May end up with a run of equal adjusted \(p\)-values, even if input \(p\)-values are distinct. These genes should be included or excluded as a unit.

Greater correction at top of table: The \(i\)th row in the table has adjusted \(p\)-value \({ n \over i } p_i\) (unless a snowball occurred).

Further filtering of set, eg by fold change, may lose FDR property.

FDR snowball example

p.adjust(c(0.05, 0.15, 0.3, 0.5), method="BH")
## [1] 0.2 0.3 0.4 0.5
p.adjust(c(0.2,  0.25, 0.3, 0.5), method="BH")
## [1] 0.4 0.4 0.4 0.5

Problems

Weak null hypothesis: that the log fold change is non-zero is not saying much. Is the fold change biologically significant?

What to do if we make too many discoveries? Temptation to set a ridiculously small FDR.

Really want to know which are the largest log fold changes.

TREAT

(McCarthy and Smyth, 2009)

"t-tests relative to a threshold"

A stronger null hypothesis:

  • "Gene \(i\) has absolute log fold change smaller than \(e\)."

Specify \(e\) to be a biologically significant amount.

Table with adjusted \(p\)-values allows reader to choose FDR.


Better but still some problems:

  • not clear how to choose \(e\)
  • may still make too many discoveries

confect ranking

Specify the desired FDR.

Present results as a "top table" that allows the reader to choose \(e\).

If there are too many discoveries, easily choose a larger \(e\) to concentrate on larger effect sizes.

confect ranking

Let \(S(e)\) be the set of genes selected by TREAT, at some fixed FDR (eg 0.05).

These sets nest: if \(e_1 > e_2\) then \(S(e_1) \subseteq S(e_2)\).

Finding \(S(e)\) for a range of \(e\) values leads to a natural ranking. Again we can present results in a "top table".

(Remaining ambiguity in ranking of genes is resolved by \(p\)-values of first set they are not a member of.)

Call the largest \(e\) for which a gene is a member of \(S(e)\) the "confect" (confident effect size) of that gene, with appropriate sign.

Example: breast cancer

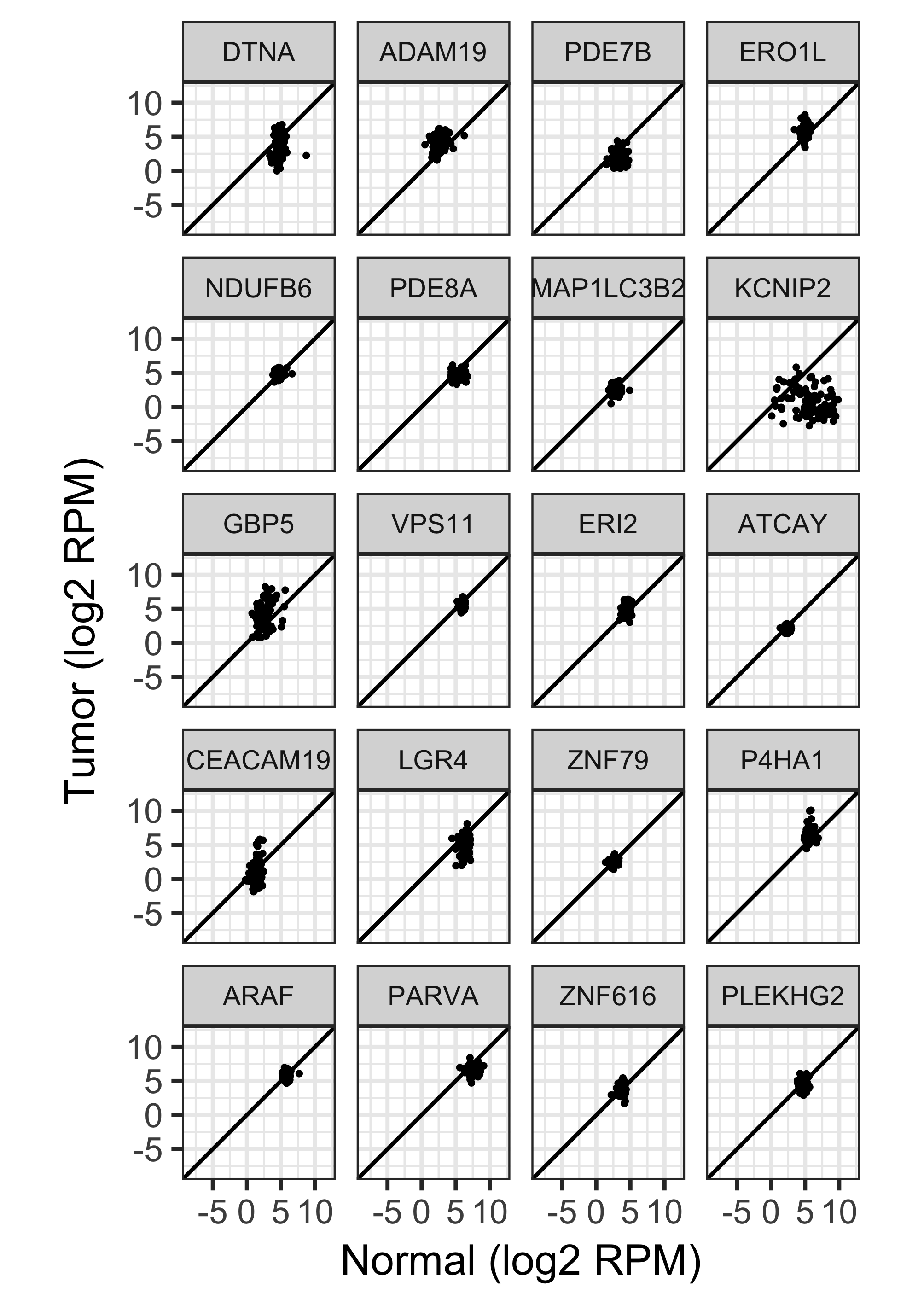97 RNA-seq tumor-normal pairs from TCGA.

Shown here, a random sample of 20 genes.

Highly heteroscedastic.

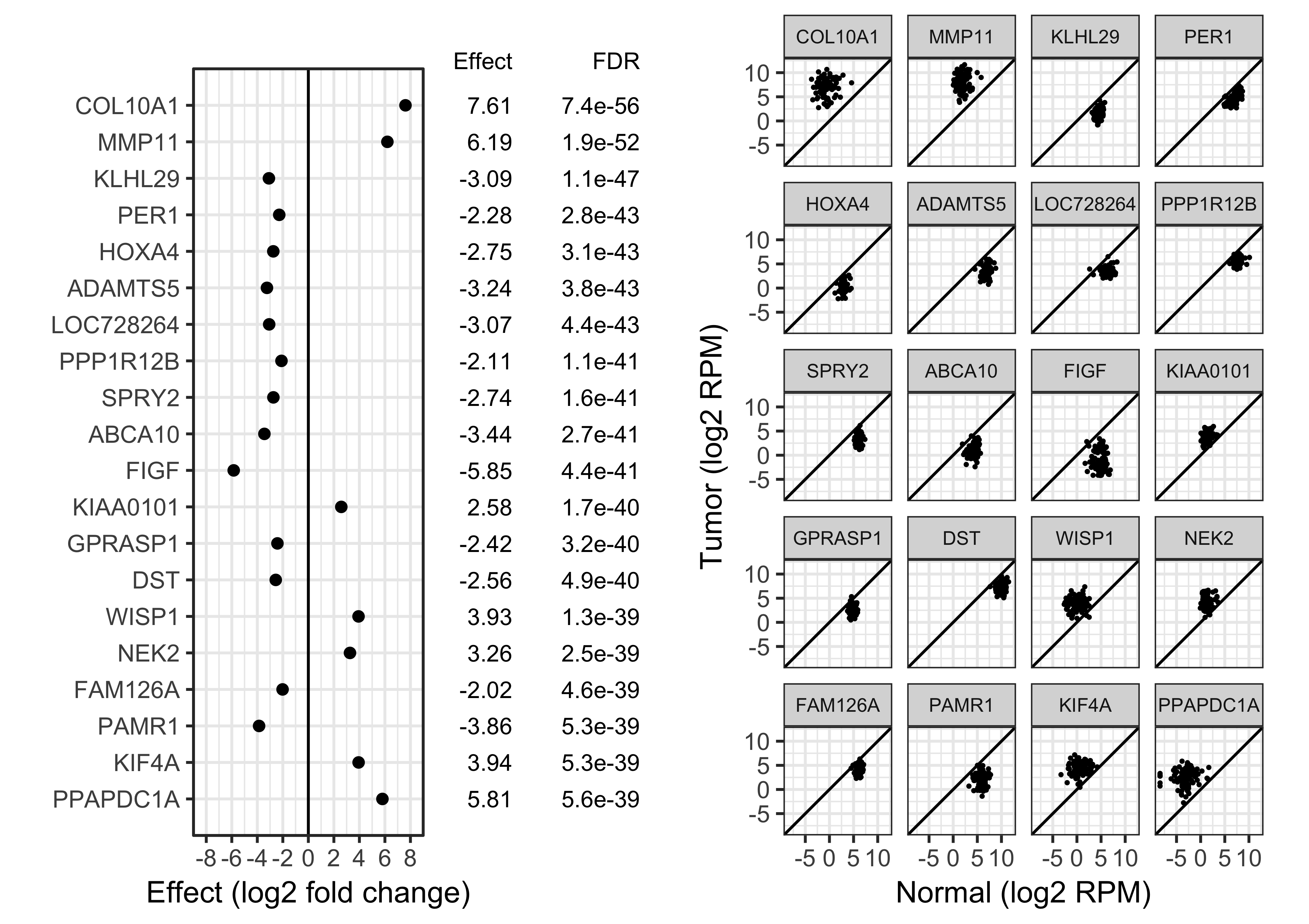
13,416 DE genes at FDR 0.05.

p-value ranking

confects ranking

Comparison of ranking methods

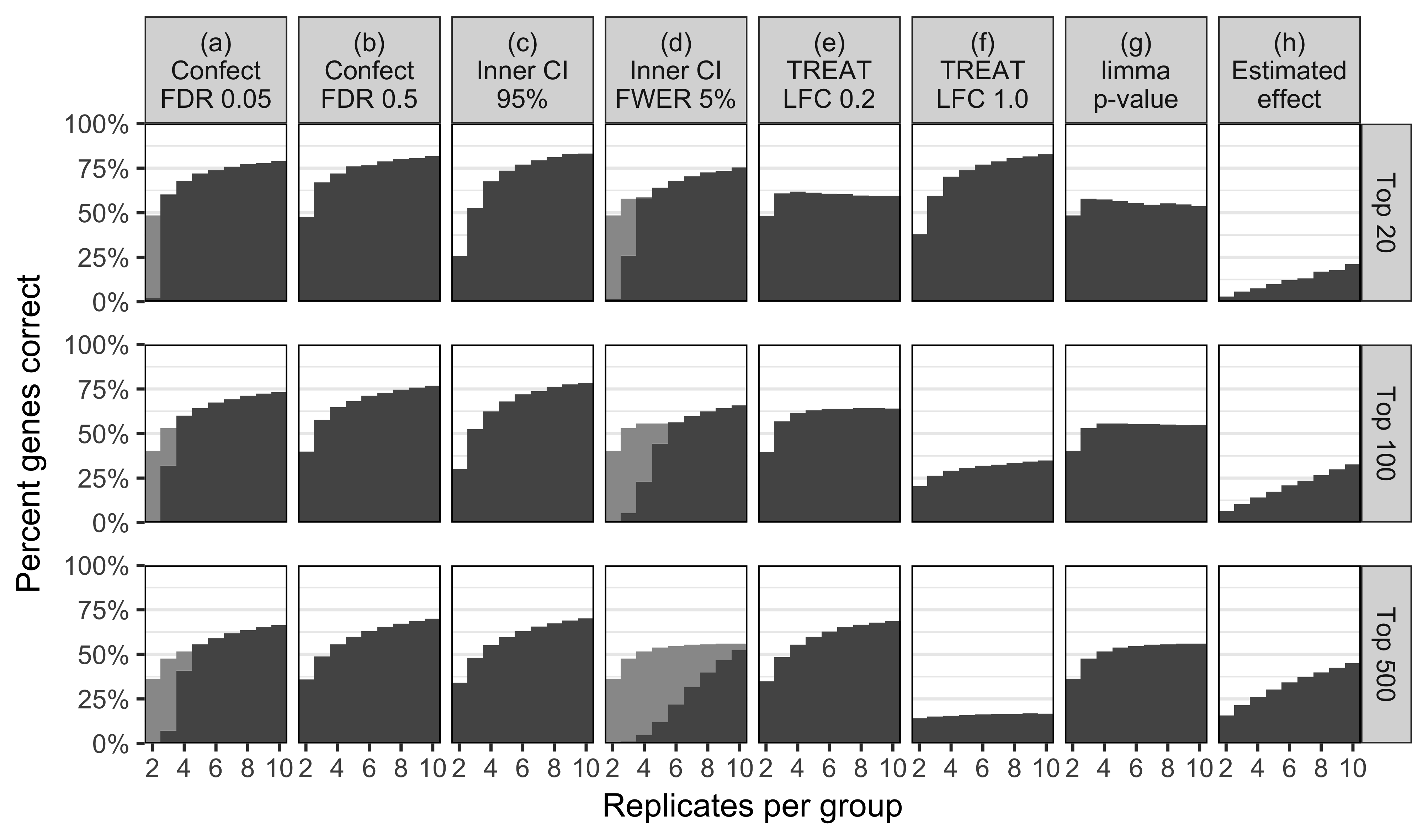
Simulate 15,000 genes \(i\)
\(\mu_{i,2} - \mu_{i,1} \sim 0.15 t(3)\)
\(\sigma^2_i \sim 0.02/{\chi^2_2}\)
(severely heteroscedastic)

Other effect sizes

Potentially useful for:

  • log fold change
  • gene set enrichment
  • interaction effects
    • shift in transcript 3' or 5' end
    • differential exon usage

Same as \(p\)-value ranking for:

  • log fold change when within-group variance is constant
  • signal to noise ratio (Cohen's d)
  • sequence alignment score

Interaction effects

Conventionally, we look for interactions of two experimental factors as a "ratio of ratios". This can be done with linear modelling of log expression levels.

Consider the interaction of two experimental factors A and B.

  • Is the response to B different depending on A?
  • Is the response due to A different in this or that subpopulation B?
    B1  B2               B1  B2
A1  20  10           A1  29   1
A2  10  20           A2  26   4

(20/10)/(10/20)      (4/26)/(1/29)
= 4                  = 4.46

Similar effect size, but first case is arguably more interesting.

Difference of proportions

Consider instead a "difference of proportions".

    B1  B2               B1  B2
A1  20  10           A1  29   1
A2  10  20           A2  26   4

 20/(10+20)              4/(26+4) 
-10/(20+10)             -1/(29+1)
= 0.333                 = 0.1

Better represents our interest level.

(Asymmetry between factors may need some care.)

Difference of proportions: zero is still zero

The difference in proportions is 0 in exactly the same cases log(ratio of ratios) is 0.

If we just look for "significance", we see no need to distinguish these two effect sizes, and we may make significant but uninteresting discoveries.

Need to care about magnitude of effect.

Example: response to salt by yeast mutant

GSE80512

Response of wildtype and mutant yeast to high salt concentration.

The mutant has a mutated histone in which post-translational phosphorylation at a certain site is prevented (thought to affect gene regulation).

Sorting by p-value

##         GENENAME     logFC    logCPM        F       PValue          FDR
## YBR021W     FUR4  1.822642  6.299541 224.8724 1.076038e-11 6.224881e-08
## YGR043C     NQM1 -1.465859  9.097715 172.7814 9.774167e-11 2.827178e-07
## YHR096C     HXT5 -1.818737 10.228356 149.9831 3.130767e-10 6.037162e-07
## YJL033W     HCA4  1.491774  4.607822 134.9086 7.402521e-10 9.885850e-07
## YBR072W    HSP26 -1.499280 11.969615 132.5314 8.544382e-10 9.885850e-07
## YOL124C    TRM11  1.271785  4.230186 124.3371 1.426553e-09 1.375434e-06
## YDR070C    FMP16 -1.280466  8.014308 117.7001 2.209317e-09 1.730566e-06
## YHR065C     RRP3  1.185455  4.371145 115.7508 2.522508e-09 1.730566e-06
## YMR011W     HXT2  1.524570 10.194933 114.8032 2.692324e-09 1.730566e-06
## YMR169C     ALD3 -1.054112 11.253244 111.5375 3.382360e-09 1.871477e-06

Sorting by p-value

Note: plots are not log scaled.

Sorting by difference-of-proportions confect

## $table
##  rank index confect effect     logCPM    name      GENENAME
##   1    850   0.18    0.2927730  6.299541 YBR021W   FUR4    
##   2   5477   0.12    0.2525727 10.194933 YMR011W   HXT2    
##   3    469   0.10    0.2196894  5.619169 YJL116C   NCA3    
##   4   1692   0.08    0.1715141  9.611573 YDR345C   HXT3    
##   5   5208   0.07    0.1596600  8.429903 YHR092C   HXT4    
##   6    884  -0.07   -0.2036980  4.193461 YBR056W-A <NA>    
##   7   3516   0.07    0.1677288  4.068022 YGR067C   <NA>    
##   8   3224   0.06    0.1456658  9.384778 YGL255W   ZRT1    
##   9   3735   0.05    0.1208114  3.753062 YLL061W   MMP1    
##  10   1888   0.05    0.1455426  8.997924 YIL162W   SUC2    
## ...
## 529 of 5785 non-zero effect size at FDR 0.05
## Prior df 6.2
## Dispersion 0.0069 to 0.021
## Biological CV 8.3% to 14.7%

Sorting by difference-of-proportions confect

3' end shift

PAT-seq produces reads at 3' ends of transcripts.

Our two interacting factors are:

  • control vs experimental condition
  • 3' end used

(((In the talk I demonstrated this with some unpublished data, so I'm not putting it up on the web.)))

R package

https://github.com/pfh/topconfects

  • Proceed from either limma or edgeR quasi-likelihood
  • Uses limma or edgeR TREAT functions for linear effect size
  • (experimental) Non-linear effects sizes, using constrained optimization
  • (experimental) Group effect sizes for end shift or differential exon usage
devtools::install_github("pfh/topconfects")
library(dplyr)
library(edgeR)
library(limma)
fit <- DGEList(counts) %>%
    calcNormFactors() %>%
    voom() %>%
    lmFit(design)


library(topconfects)
confects <- limma_confects(fit, coef=test_coef, fdr=0.05)

Conclusion

Demonstrated a simple twist on the TREAT method.

  • better ranking of genes by interest level
  • confidence bounds on effect size make biologically meaningful claims
  • no more adjusted p-values, no more ad-hoc balancing of p-values and log fold changes
  • freedom to choose a meaningful effect size

Acknowledgements

RNA Systems Biology Laboratory

Traude Beilharz

Andrew Pattison

Monash Bioinformatics Platform

David Powell






The results shown here are in whole or part based upon data generated by the TCGA Research Network: http://cancergenome.nih.gov/