We can approximately factorize a note n (given in semitones) with:
12a + 19b + 28c = n
Where a, b, and c are integers. This is a "Diophantine" equation. It has multiple solutions, representing multiple possible factorizations. These solutions turn out to form a two-dimensional grid in the three-dimensional (a,b,c) space.
We can change our parametrization of this space so that one dimension is normal to the grid, and two of the dimensions are co-planar to the grid and wrap onto themselves.
We can do this, but is it a worthwhile exercise?
Consider the tune (selected entirely at random) Buffens from Arbeau's Orchesography. The top line is Arbeau's melody, the bottom line is a counterpoint of my own invention.
Buffens MP3
/ Newer version
/ Newer version, slower

Let's visualize this in the three dimensions (one of unlimited extent, and two wrapped on themselves). Green is Arbeau's melody, blue is my counterpoint.
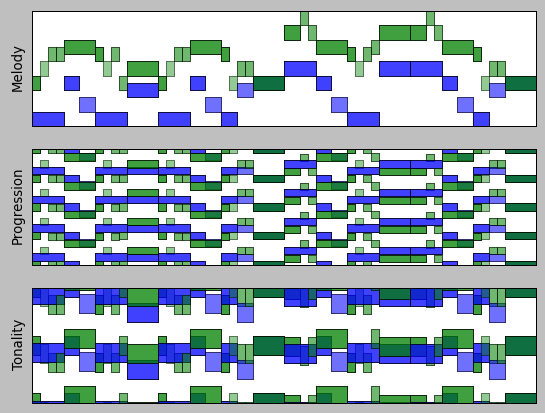
I've named the first dimension "Melody", since it's a straightforward mapping of the semitone value. You can see Arbeau's smooth melody line. The inspiration for this is The Music Animation Machine.
The second dimension I name "Progression", since this is what you can see in it. Roughly speaking, it has to do with movement by perfect fifths (factors of 3). Upward motion creates a pleasurable tension, and downward motion is conclusive.
The third dimension I name "Tonality", since the notes of the diatonic scale are tightly clustered in this dimension. Roughly speaking, it has to do with movement by major thirds (factors of 5). If key changes were present in a piece, they would be seen in this dimension.
Ok, so. Let me try to explain the C Major diatonic scale. I'm going to show an extract from the circle of fifths, and another extract below that, so that major thirds are lined up.
(B F# C#)
... G D A E B F# C# ...
... Eb Bb F C G D A ...
II IV I V
?
-- note the similarity to the Stradella bass system on accordions.
Imagine a line running from D on the first line through D on the second line. Movement along this line is the progression dimension. Movement vertically away from this line is the tonality dimension. So here F# and Bb are furthest from the line, and can be used as a brief departure from the tonality.
Below this I've named some chords. Each chord applies to the block of four notes above it. For example, I has E, B, C and G. Progression likes to move left, descending by fifth. The chord marked II you get some bonus notes to play with, F# or Bb or maybe even C#. Or you can just stick to I-IV-V-I, that is perfectly fine apparently.
Using both notes on a "/" diagonal in a harmony, such as C and B, would stretch the tonality a bit far (unless that's the effect you want). However for a sense of fullness in the tonality you do need notes from both lines, and for a sense of fullness in the progression dimension you want notes from the left and right columns of the block. So in this sense the minor third (eg E-G) is the nicest harmonic interval, in that it gives you fullness in all dimensions without stretching any too far.
and maybe a little